若曲线y=x^2+1和直线y=-x+3围成的区域，再绕X坐标轴旋转一周，形成一个立体，计算该立体的体积。 如图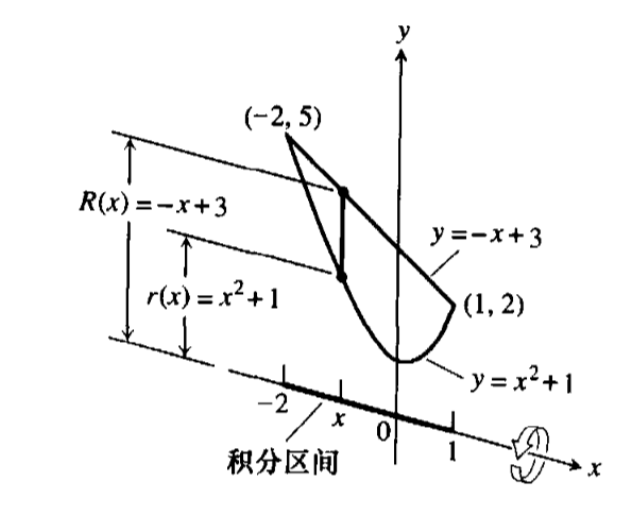： 先计算出所要求的在X坐标轴的积分上下限为[-2,1]。仔细分析可知，外部的大圆半径为R(x)=-x+3，r(x)=x^2+1。大圆R(x)-r(x)即为实际围成的面积: 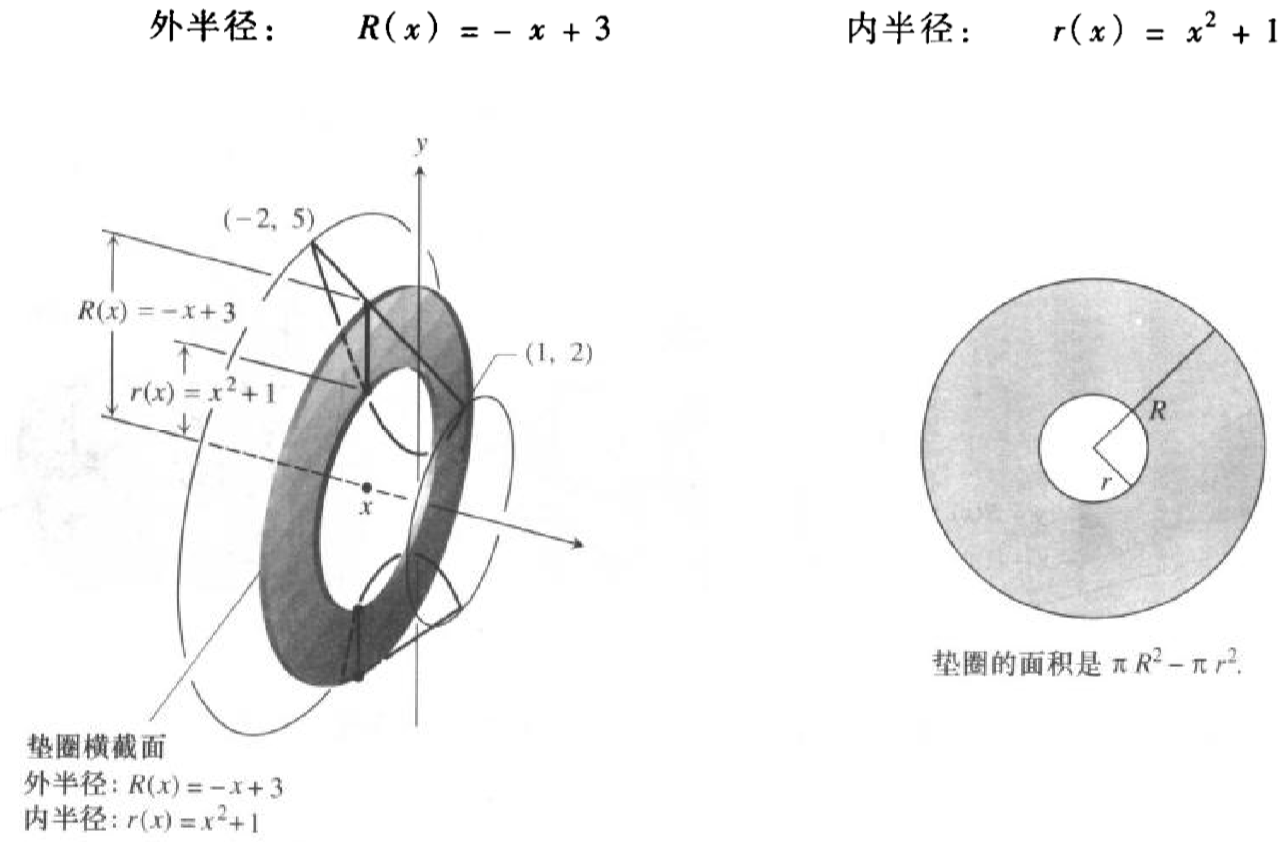根据立体面积积分公式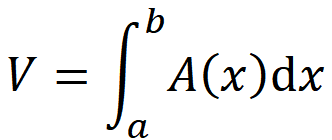：   其中，A(x)为立体截面面积。 可知问题最终求解的体积为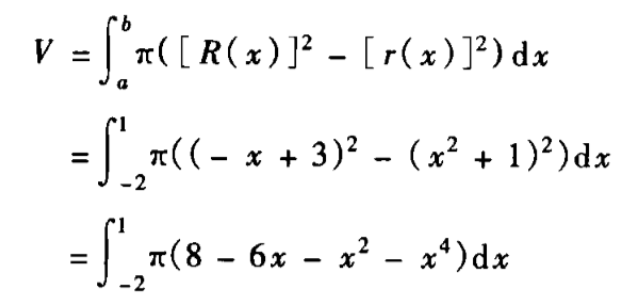： 用matlab计算：

syms x f;      f=pi*(8-6*x-x.^2-x.^4);V=int(f,[-2,1]) V = (117*pi)/5

体积为：(117*pi)/5 ,其中pi为π。